Do aspects of Shodan data – data about Internet of Things (IoT) devices and systems – demonstrate ‘long tail’ qualities? Data showing these qualities sometimes also go by the name of having a ‘Zipf distribution‘, following a power law, or behaving according to the Pareto principle. If there is in fact a reoccurring relationship or curve that occurs across aspects of IoT data, that might offer some insights into how to categorize or classify aspects of IoT systems. For managing risk around IoT systems implementations, our current ability to classify and categorize these systems is sorely missing. Potentially, it could also offer predictive capabilities regarding elements of the Internet of Things phenomena.
To take an initial swing at it, I narrowed the question down to:
Do the frequencies of occurrences of particular ports (services) in an organization, or other Shodan data set, behave in a repeatable way?
Long tails & power laws
The concept of long tail behavior was popularized in Chris Anderson’s 2004 Wired article and it has entered popular vernacular in the years since. What Anderson articulated was that aspects of many systems or sets of data are characterized by the observation that there are a lot of a few types of things and then a rapidly dropping number of other types of things — but there are a lot of those other types. Anderson used the example of record sales — there are a relatively few mega-hit songs, but there are a lot of non-hit songs and record companies were learning how to capitalize on this observation. This is the long tail.
Another example is early ‘long tail’ work attributed to George Zipf with his analysis of word distribution frequencies in any particular text. He found that if you:
- counted how often each word appeared in a text
- ranked each word so that the word with the highest count got the highest rank (i.e. #1) and down from there
- plot the results in a graph
then you find a curve that shows that a few words show up a lot.
For example, the words ‘the’, ‘be’, and ‘to’ show up a lot (1st, 2nd, & 3rd in a ranked list) and words like ‘teeth’, ‘shell’, or ‘neck’ shows up around 1000 places down the list. From the first few spots in the ranked list, the frequencies of other ranked words fall off quickly — but there a lot of those ‘other’ words. Further, this curve is a power law which looks a bit like y = 1/x. Variations include multiplying 1/x by something and raising x to some exponent. (For Zipf relationships, this exponent is often close to 1).
Yet other Zipf relationships are found in studies of populations of cities data and website references.

Ranking city population sizes also follows Zipf-like relationships (the loglog plot is fairly linear)
Power law relationships in IoT data?
John Matherly, founder of Shodan, has been collecting data on IoT sorts of devices for years. He scans all publicly accessible IP addresses for particular ports for Internet of Things or Industrial Control systems including things like power plants, video cameras, HVAC systems, and others.
I have a particular interest in how IoT data shows in higher education IP address spaces, so I analyzed large subsets of data in some of those institutions. To do this I queried for data from those publicly facing IP spaces in the organization and exported it to a json format. (Shodan also offers an XML version, but it is deprecated). From the downloaded data, I used Python scripts to clean the data a bit, count how often each port occurred, and then rank them by organization. Finally, I used the Python module matplotlib to plot the results.
This is similar to the word frequency analysis approach above where, for a set of data:
- Count the number of occurrences of each port (service)
- Rank the ports so that the port (service) that occurs most frequently gets the highest rank
- Plot the results
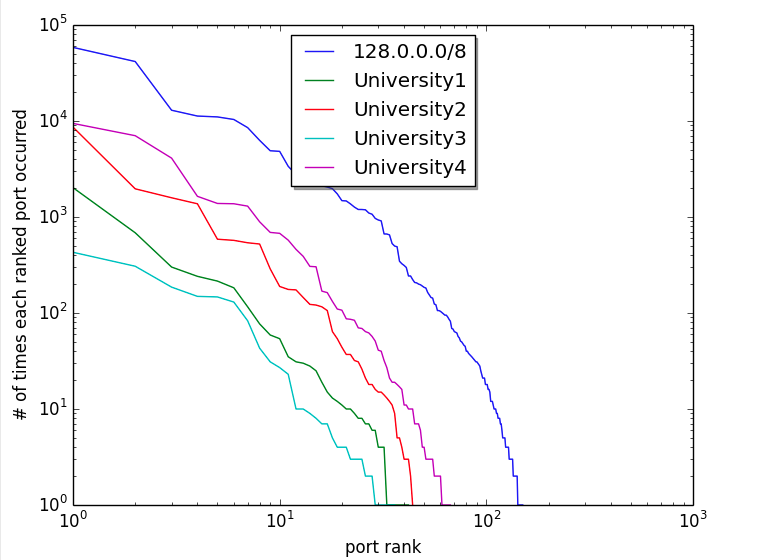
Like word frequency data in Zipf studies, a plot of frequency of occurrence of each port vs rank of each port’s frequency yields a curve that drops off so fast that it is hard to discern nuanced information. However, the fact that it does drop off so fast let’s us know something at a glance that is similar to Zipf data — a very few ports occur most often and a lot of ports have a few occurrences.
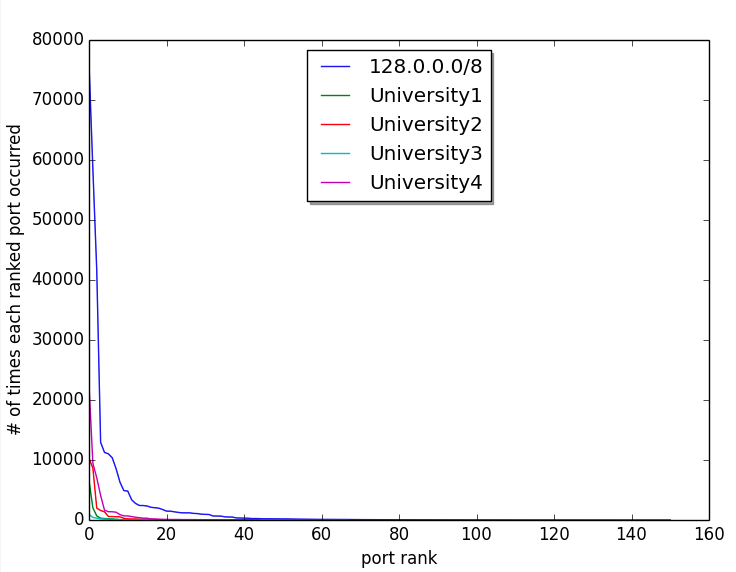
4 universities and 1 (organizationally) arbitrary & large) set of IP addresses on normal (non-log) plot
What gets more interesting visually is to plot that same data on a log log scale. This kind of brings the curve out to where it’s easier to see.
Zipf-like data can follow the relationship of y = 1/x almost exactly for much of the range. (This is part of why word frequency, city population data, etc is so intriguing.) So when plotted on log log, much of the line looks almost straight – slope of 1 (ish).
A log log plot of university IoT data doesn’t yield a straight line, but sort of a bulging out line. If you were standing on the graph way out to the right and up and looking toward the origin, it would appear convex. So this isn’t Zipf in the traditional sense — the log log plot is not linear.
However, they do look similar. University1 looks roughly like University2. University2 like University3, and University3 like University4, etc. The curve roughly retains its shape regardless of the school, though the school sizes are different (or at least the number of public IP addresses are different).
Maybe the organization doesn’t matter?
Also plotted are the results from a search on all of the IP addresses in the 128.0.0.0/8 range (using CIDR notation). This curve, though bigger and slightly smoother, has roughly the same shape as the others. The main thing that separates it from the others appears to be magnitude (number of IP addresses sampled). It appears that there is nothing particularly unique about an organization that drives this curve shape — a similar shape appears even if a set based on a numerical range, regardless of organization, is chosen.
It will be interesting to see if, as IoT device count grows, the curve changes shape. Will the set of IoT devices across the globe continue to communicate mostly over the same ports/services as those currently in use, keeping the same shape? Or will new ports/services/enumerations show themselves as IoT device proliferation continues, changing the shape? By analyzing ranking relationships over time and between organizations, this approach could provide some insight into helpful categorizations for risk analysis.